编者按:为进一步促进学术资源共享与学术交流合作,快速传递和分享各研究领域的高质量学术论文,确保师生能够及时获取最新研究成果及前沿学术动态,自动化学院特开设“学术快讯”新媒体专栏,旨在通过精心筛选和整理,致力于将最新的、具有影响力的学术文章呈现给读者。本期推荐论文:《基于分数阶高斯-埃尔米特矩的图像分析》。
一、中文题目:基于分数阶高斯-埃尔米特矩的图像分析
二、英文题目:Image Analysis by Fractional-order Gaussian-Hermite Moments
三、作者信息:杨波,史晓娟,陈小锋
四、发表刊物:IEEE Transactions on Image Processing (IEEE T-IP)
五、论文索引信息:DOI: 10.1109/TIP.2022.3156380
六、论文简介:矩和不变矩是图像处理领域内的经典特征描述子。当前研究表明分数阶矩具有显著的图像表示能力。埃尔米特多项式的定义区间为负无穷到正无穷。这种无限型区间导致无法通过常规思想设计分数阶高斯-埃尔米特矩。在考虑离散信息处理的基础上,论文令埃尔米特多项式的定义区间为有界区间,利用不断递减的标准差参数保持多项式的正交性,在此基础上设计出分数阶高斯-埃尔米特矩。此外,论文提出了对比度、平移和旋转不变量。图像重建、图像识别、噪声鲁棒性和兴趣区域特征提取等实验反映所提出的分数阶矩及其不变量具有良好的特征分辨力和的噪声鲁棒性。
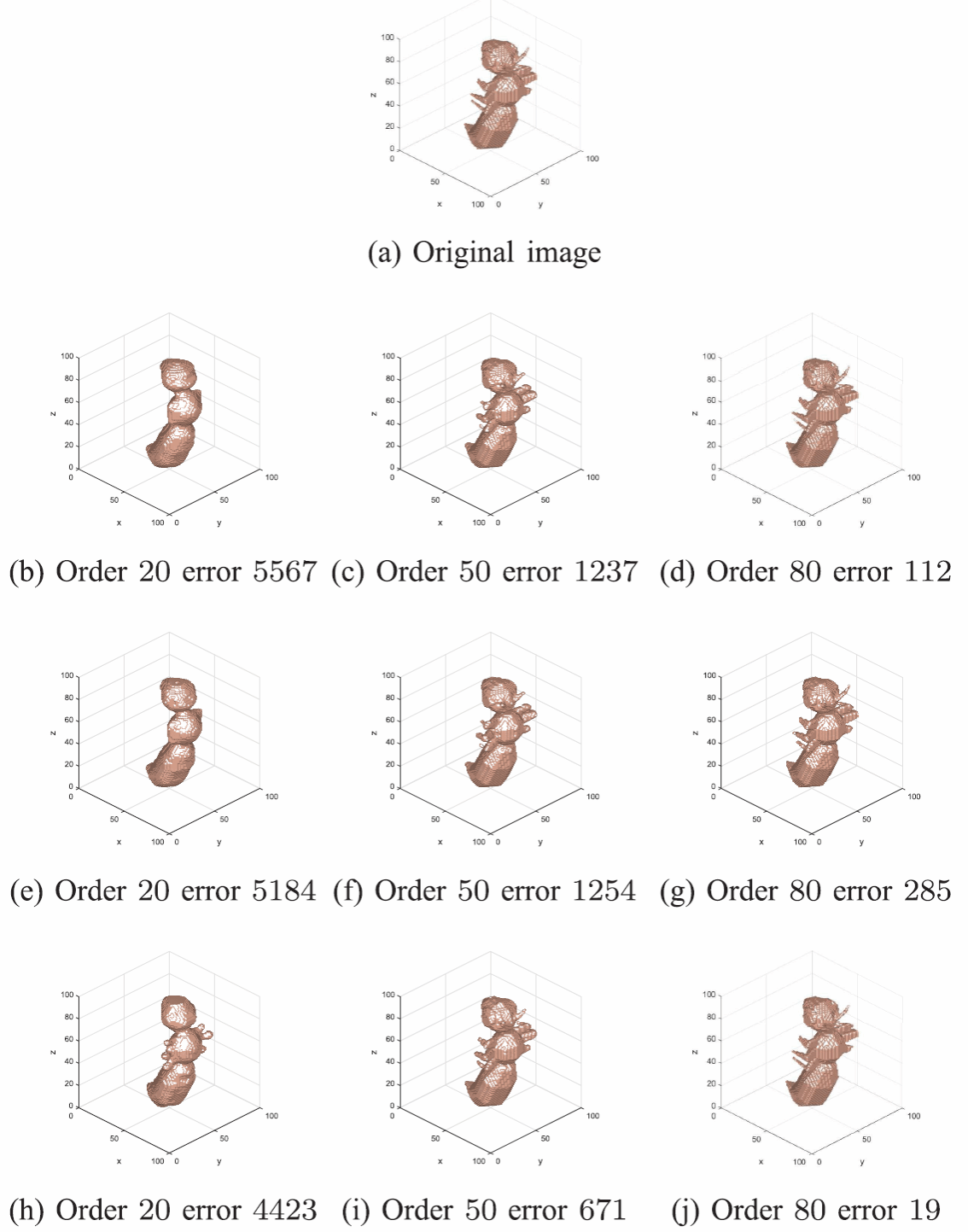
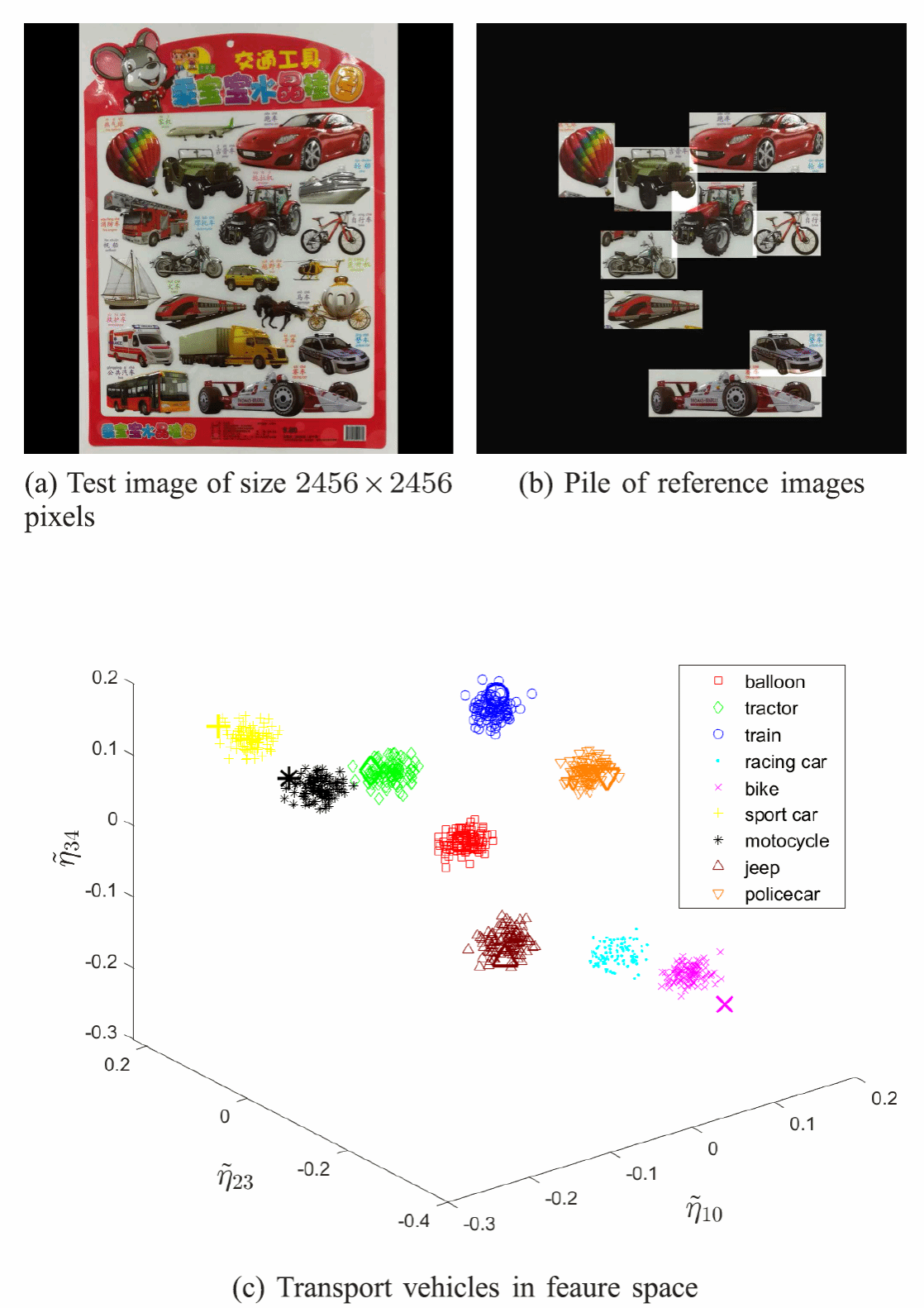
图1 基于不同正交矩的三维图像重建 图2 基于分数阶高斯-埃尔米特矩的目标分类
来源:杨波
审核:王小旭



